作者の谷甲州自身の言葉によると、『天を越える旅人』は「アインシュタイン以降の宇宙論を仏教的な世界観で再構成できるだろうか」という領域に踏み込んだ作品である。
そこで、「アインシュタイン以降の宇宙論」をキーに『天を越える旅人』を読んでみよう―もしくは逆に『天を越える旅人』をキーに「アインシュタイン以降の宇宙論」を読んでみよう―というのが、この稿の目的である。
というわけで、話は核心である、ヤシュティの問いからはじめよう。
『認識〔ブッダ〕とは何か。法〔ダルマ〕と智慧〔サンガ〕の統合は可能か。可能だとすれば、その方向を…』(380ページ)
ヤシュティの問いを、ミグマはこう解く。
『時間と空間の概念を統合することは可能なのか。物体とそのエネルギー―あるいは力と運動の法則は統合が可能なのか。すべての情報を記述する式は存在するのか。存在するとすればそれによって現在は再現できるのか。そして未来の出来事を予言できるのか。』(381ページ)
このヤシュティの問いは物語のクライマックスの部分であるが、物語の中段部分、ミグマが曼陀羅に入り込むところでも、この問いかけは行われている。
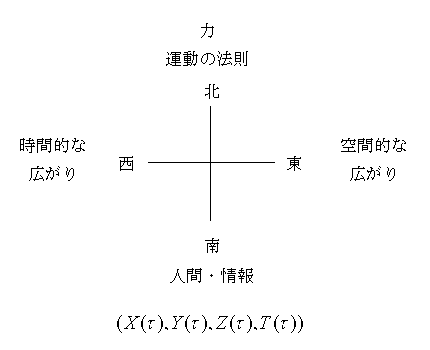
ミグマは曼陀羅の構造を下のように解く。

ヤシュティの問いはこの「東」と「西」を統一する「北」を求めよ、ということになる。「南」はどこへ行ったのか?―「統一する」の主語が「南」、つまり、「人間・情報」であるところのミグマであるとも考えられるし、「東」(空間)「西」(時間)「北」(法則)の中に産まれるのが「南」(人間)であるとも考えられる。
時間と空間の融合、物体とそのエネルギーの統合というのがミグマに与えられた問いであるが、その問いにアインシュタインはどう答えているか。
相対性理論では、時間1次元と空間3次元を足した4次元時空の中での軌跡として運動を考える。
この「運動」は次のように表される。
(X(τ),Y(τ),Z(τ),T(τ))
* このXYZは空間の座標、Tは時間座標である。τは、運動している物体自身の感じる時間(「固有時」)である。
例えば物体が静止している時、XYZは変化しない。そして、Tはτと等しくなる。静止している物体の感じる時間は、普通の時間そのものだからである。
つまり、τが1秒増えるとTも1秒増える、というふうに変化していく。
別の言い方をすれば「静止している物体は時間の方向に速さ1で進む」ということだ。
では、運動している物体の速さはどうなるのか。
たとえばX方向に動くならば、X方向の速度は0でなくなる。しかし、ウラシマ効果という名前でよく言われるように、移動すると時間が遅れる。つまり、τの進みがTの進みに比べておそくなる。逆にいえばτが進むのに比べてTの進む割合が大きくなる。つまり、T方向の速度は1より速くなるのである。
実はこの時
![]()
が常に1になるように、X方向の速度とT方向の速度の関係が保たれている。この量の平方根は「4次元時空での速さ」と呼ばれる。X方向の速度とT方向の速度が増えるが、上で表した4次元時空での速さの二乗は常に1なのである。
ただし、ここで、(X方向の速度)を測る時、X方向を測るものさしは、「1光秒」で測っている。『この世界に常なるものは何もないのだから、空間や時間を絶対的なものと考える必要はないのではないか。それなら時間と空間の関係―光速度を一定と考えて、ほかの量を定義すべきではないのか。』(392ページ)とミグマは考えているが、相対論的には、長さを「光秒」という、時間を基本にした単位で測ることは上のような理由で意味がある。
ところで、『天を越える旅人』の中の光速度は、一刹那に五七〇由旬だそうである。『須弥山と極楽』(定方晟/講談社現代新書)によると、一刹那は七五分の1秒、一由旬は約七キロとなっている。これでは光速度が四二七五〇キロ、ということになって全然合わないが、由旬や刹那の実際の長さには諸説あるらしいから、合わなくても別によいのだろう。
それはさておき、ここでは秒と光秒という「自然」な単位(4次元の話をする時には自然なのである)を取っておけば、4次元時空の中での物質の速度は1に拘束されている。これが物体の速度が光速を越えることができない理由である。
一見、上の式を見ただけでは、(X方向の速度)がいくら速くなっても、(T方向の速度)がそれに応じて速くなればいいんだから、いくらでも速度は速くなれるじゃないか、と思うかもしれない。もちろん、それはその通りである。大事なことはこの(X方向の速度)は、τで測っての速度(すなわち、τが1秒増える間にX方向に動く距離)である、ということである。外から見た、実際の速度はTで測っての速度(Tが1秒増える間にXがどれだけ増えるか)なのである。これは、(τが1秒増える間にTがどれだけ増えるか)で割ってやることによって修正できる。つまり、(Tが1秒増える間にXがどれだけ増えるか)は、

として計算できる。これは、1を越えられない(分母の方が必ず大きいから)ので、Tで1秒あたりにX方向に1光秒以上進むことはできなくなる。
加速する、ということは、4次元時空の言葉で言えば「長さが1のまま、回転させる」という事に等しい。これがアインシュタインの手になる(正確には、アインシュタインの理論を解析したミンコフスキーの手になる、というべきか)4次元時空という形での時間と空間の統一である。
この(T方向の速度)はどういう意味を持つか、というと(すでにお判りの方も多かろう)これが「エネルギー」なのである。
正確に言うと、(静止質量)×(T方向の速度)がエネルギーであり、相対論的質量である(普通、エネルギーと質量は光速度の2乗分違うのだが今は光速度は1なのだ)。静止質量と相対論的質量は違うものであるから区別しなくてはいけない。相対論的質量は加速により増大するが、静止質量の方は運動によって変わったりしない。
だから、ミグマが見いだしたように、
『――つまりエネルギーと質量は等価なのか。
物体の奇妙なふるまいをみるうちに、ミグマはその事実に気づいた。物体を加速させたときは質量の一部をエネルギーに変換していたのだが、物体のもつエネルギーもまた質量を変化させるようだ。』(393ページ)
ということになる(ただし、この文章の最初の「質量」は静止質量で、二個めの「質量」は相対論的質量と解釈すれば)。動かすことは同時に(T方向の速度)すなわち相対論的質量を大きくする、ということでもあるからである。
ただし、ここで気をつけなくてはいけない事がある。もし、ミグマが静止した物体の質量をすべてその物体のエネルギーに変換して加速することができたのならば、その加速による質量の増大はちょうど変換された質量を補うことになる。つまり、下の図のようになる。

このようになる理由は、
(静止質量)×(T方向の速度)
がエネルギーすなわち相対論的質量だからである。
「物体を加速させたときは質量の一部をエネルギーに変換していた」というのは、「(静止質量)を減らして(T方向の速度)を増やした」ということになる。
ミグマの言葉の中で「物体のもつエネルギーもまた質量を変化させる」の<質量>は静止質量でなく、相対論的質量の方であろう。
エネルギーは実は保存するので、もしエネルギーを加速する物体自体からと
ったのだとすると、相対論的質量の方は変化しないのである(静止質量の方は減る)。
実際、ミグマは『その核の一部をとりくずし、エネルギーに変換して加速した。』(392ページ)とあるので、この時、相対論的質量は保存する筈である。それなのに、『加速によって実体をくいつぶしているにもかかわらず、観測される物体の質量が次第に増大していったのだ』(392ページ)というのはちょっとおかしい。おそらく、ミグマは無意識のうちに力を加えて、エネルギーを与えてしまったのに違いない…。
ところで、上の話には一つ制限がついていた。「もし、ミグマが静止した物体の質量をすべてその物体のエネルギーに変換して加速することができたのならば」という制限である。ところが、実際にはこれはできない。なぜならこの世界には運動量保存則、というもう一つの重要な保存則がある。一つの物体を加速したら、かならず別の物体を逆に加速しなくてはいけないのである。そのため、エネルギーは加速される物体と反動を受ける物体に分配されてしまう。

『天を越える旅人』のこの部分では、反動を受ける物体は書かれていない。もし反動を受ける物体がミグマだったのだとすると、ミグマと物体の間に力が働いていたことになるので、「ミグマは無意識のうちに力を加えて、エネルギーを与えてしまったのに違いない」という予想は実にもっともらしいのである。
ところで、本来の問題の問いの最後のもの、『すべての情報を記述する式は存在するのか。存在するとすればそれによって現在は再現できるのか。そして未来の出来事を予言できるのか。』の答えはどうなるのか。
まず、力の式に関しては、ミグマは重力の方程式(ニュートンの万有引力の法則だろうか、アインシュタインの一般相対論だろうか?)は見つけたようだ。しかし、他の力を考えて統一することには躊躇を感じてやめてしまう。残念である。実際には電磁力と強い力と弱い力、と知られているだけでも後3つも力があるというのに。もちろん、天体の運動を考えるには、重力だけで充分なのであるが。とはいえミグマは曼陀羅の中で、力が分裂していくところは見ているのであるが(その部分は189ページであるが、宇宙の始まりからインドの南方に軌道エレベーターができて人類がいなくなり宇宙が冷えきる…という悠久の時間が1ページの中に詰め込まれている)。
現在の素粒子論では、この4つのうち、電磁力と弱い力はもともと一つの力が分岐したものであることがわかっている。そして、強い力もきっとこれら二つから分岐したものであろう、と思われている。最後の一つ、重力も元は同じものだったのかどうかは、現在皆目わからないが、そうであって欲しい、と多くの人が思っているようだ。
それはさておき、上に述べたような記述をしていけば、物体の運動は4次元時空の中に引かれた線の形に表せる。物体に加えられる力を計算してそれに対応して線を引いていけば、その物体の運動は記述できる。物体の数が多くなっても、一個一個に働く力を計算することができれば、現在も過去も未来もわかる。曼陀羅の東西南北で言えば、「東」と「西」は4次元時空である。そして「北」はその4次元時空に線を引く時の引き方である。そしてその線のからまりの中に「南」が産まれるのである。
しかし、未来がわかる―というのは古典力学の段階でのことで、これが量子力学の段階に入ると、「位置と運動量を同時に決定できない」という不確定性原理に阻まれ、完全な予測が不可能になる。このあたりをミグマが気がつくのが、
『だが、そんなことは本質的に不可能だった。なぜなら観測者の存在によって、物体の運動が乱れてしまうからだ。恒星のような大質量ならともかく、微少物体のもつ情報は観測者の存在によって変質してしまう。未来情報を式によって表現するのは不可能なのだ。』(395ページ)
のところである。
観測者はある物体の、位置もしくは運動量を測定しようとする。だが、位置を正確に測定すればするほど、運動量が不確定なものに変わってしまう。逆に運動量を正確に測定すると、位置が不確定なものに変わってしまう。
これが『観測者の存在によって変質してしまう』の意味するところである。残念ながら、この性質により、未来情報を完全に式で表現することはできなくなる。量子力学では、アインシュタインが嫌ったように、「確率を計算する」ことだけができる。ミグマは(そして、我々は)そこまでで満足しなくてはいけないのである。
ここで、量子力学の穴の部分をさらにつついていくと、『エイダ』(山田正紀)だの、『時間的無限大』(バクスター)だのが扱った「観測問題」という穴蔵にはまりこむことになる。この点、ミグマはあっさりしたもんで、穴蔵は避けて進んでいる(その後に待つものの方が大事だったからだが)。
ところで、もう一つ、宇宙観という点で『天を越える旅人』の中に出てくるキーワードがフラクタルである。曼陀羅の中にフラクタルに特徴的な自己相似性があらわれる、という話があるが、『密教とマンダラ』(日本放送協会)の著者の頼富本宏氏は『マンダラに関心を持たれた方からのお手紙の中で、マンダラの基本的な円形や四方形などの構造に対して、「入れ子構造」や「フラクタル理論」などの斬新な御意見をいただくことがある。』とこの本の中で述べているので、こういう感想はみんなが持つものらしい。
フラクタルの本質は入れ子構造というより、「観測の精度(スケール)を変えると、どんどん微少構造が見えてくる」という点にある(同じ微少構造が繰り返し現れると入れ子構造となる)。自然がフラクタル次元を好む、というのも、結局このような構造がよく見られるからであるが、「極美の世界の中にまた世界がある」という宇宙観はSFでもお決まり(『金剛石の乙女』『フェッセンデンの宇宙』などなど)であるが、それだけお決まりになるということは、宗教に依存せず、人間の宇宙観によく結び付いているのだろう(最近それがフラクタルという用語で説明できるようになってよかった…というべきなのかどうか)。
まだ他の3つの力を解析してないとはいえ、重力の法則と相対論と量子力学はマスター(?)したミグマが、こことは全く法則の違う他の宇宙へと旅立つところで『天を越える旅人』は終わる。
この時かいま見るもう一つの宇宙では重力定数の値がかなり大きいらしい(偶然だろうけど、バクスターの『天の筏』と類似している)。重力定数の大きさは、恒星の温度に非常に大きな影響をおよぼす。重力が強いと恒星中心での圧力が大きくなるため、小さな星でも核融合を起こすのに充分な圧力が得られるのである。
なお、ホーキングや佐藤勝彦などの宇宙の多重発生の理論などでは、やはり宇宙がたくさん(三千世界ほどかどうかはしらないが)の宇宙が発生する、と言われる。その理論の中でも、物理定数の値が違う宇宙、いや、そもそも、先に述べた、力の分岐の仕方さえ全く違うような宇宙が平行存在する可能性もある、と指摘されている。この宇宙で物理定数や力がこんな形になったのは、単なる偶然であるかもしれない、という考え方である。
転生を繰り返しながらの「修行」であれ、数式を巡らしての「研究」であれ、神ならぬ身の人間が自分が住んでいる以外の他の宇宙のことまで知ろうとは、随分傲慢なことである(あ、だからミグマは死んでからいくのか)。
しかし、もしこれらの別の宇宙を見ることができるものなら(そして見た後、たとえ死んででもこの世界に帰ってこれるものならば)、見せて欲しいものだと私も思う―ミグマのように。