宇宙航行の基礎について、もう少し。宇宙での広義の加減速（以下、軌道修正と呼ぶ）は、スラスタ噴射にほぼ頼り切ることになるわけだが、その際きわめて重要なことは、噴射口
『軌道傭兵』を根っから文系人間が読んで一番判りにくいのは、衛星軌道上での航行や物体運動の有様ではないだろうか。ＳＦファンたるもの、地上と宇宙での飛び方の違いくらいはまずは知っているものだが、衛星軌道上での航行（以下、軌道航行と称する）というのは、さらにまた勝手が違うものだ。
例えば、同じ軌道上に二つの飛翔体があるとする。後方の飛翔体が前方のすぐ近くにいくにはどうすればよいか。
実は、後方に噴射推進装置を噴かして加速すると、大変無駄が多いのだ（よほど近くなら別だが）。正解は、まず前方に噴かして減速し、低軌道でしばらく慣性航行してから今度は加速することだ。（この件の詳しい解説は後述）
以下、軌道航行について、順を追って解説してみよう。
『たとえ鳥でも永久に飛び続けられはしない』……のは地上だけ
甲州ファンにとって、宇宙と地上（大気圏内）での飛び方の違いは、常識であろう。とはいえ、その違いを整理することから始めるのが順序というものだ。
まず確認しておかなければならないのは、『飛ぶ』という概念自体が、宇宙と地上では違うということだ。地上では、「飛んでいる」物体は力を加えなければいずれ落ちて止まる。しかし宇宙では、同じ進路と速度のままに飛び続ける。地上では、重力の作用と空気抵抗によって地表に物体の進路がねじ曲げられるため飛び続ける事自体にエネルギーが必要だが、宇宙ではそうではないのだ。厳密さをやや欠く言い方をすれば、地上では「止まっている状態」が基本。宇宙では「真っ直ぐ飛んでいる」状態……慣性飛行が基本となるわけだ。
次に、広義の加減速……速度と飛ぶ方向を変える方法の違いを確認しよう。宇宙では、空気抵抗を使ったプロペラや鳥のはばたきのような推進手段は使えないし、方向を変えるのにも宇宙では空気抵抗を使うことが出来ない。宇宙で「飛ぶ」手段（広義の加減速の手段）は、このようにほとんど噴射推進装置
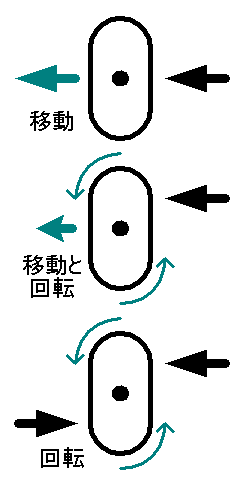
下手に噴かせば目が廻る
宇宙航行の基礎について、もう少し。
宇宙での広義の加減速（以下、軌道修正と呼ぶ）は、スラスタ噴射にほぼ頼り切ることになるわけだが、その際きわめて重要なことは、噴射口
軌道上じゃぁ、また違う
いよいよ、軌道航行（衛星軌道上での航行）解説の本編である。
もちろん軌道航行も基本的に宇宙航行のカテゴリーの一つである。ただ問題は、軌道航行は大質量の大きな影響化で行なわれるため高速の円運動（楕円運動）が基本となることだ。従って、
慣性航行は直線的ではなく、特定の円または楕円（『軌道』）上を周回することになる。また、スラスタ噴射も、「どちらに向けて」噴射するかによって軌道修正の方向が違ってしまう。
あるいはこう言い替えてもいいかもしれない。軌道航行での軌道修正（加減速）はすなわち軌道遷移である。つまり、ある円（楕円）軌道から別の円（楕円）軌道に移ることだ*2。だから、噴射した結果どんな軌道に移行することになるのかが唯一の問題といえよう。
噴射方向と軌道遷移の関係を解説する前に、まだ二つ解説すべきことがある。
まず、円軌道における軌道高度と軌道速度*3の関係を解説しよう。
円軌道の軌道速度は、高高度ほど遅い。高軌道ほど地球から遠ざかるだけ受ける重力が小さくなり、それとつりあう遠心力も小さくなるからだ。しかも軌道高度が高いほど一周の距離は長くなるので、一周するのにかかる時間は高高度軌道
になるとどんどん長くなる。例えば高度２００㎞なら約１時間半なのに、高度３６０００㎞（静止軌道の高度）なら２４時間となる。
次に、楕円軌道においての主だった術語を解説する。
まず、楕円軌道という言葉だが、しばしば長円軌道ともいい『軌道傭兵』中ではほぼそれに統一されているので以下は長円軌道という言葉を使う。
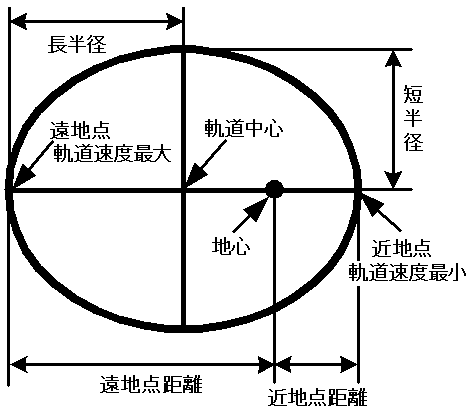
軌道がつくる楕円（長円）の最も長い差渡しを長軸といい、その長さの半分を長軸半径（または長半径）という。また長軸の中点を軌道の中心という。長軸上には、軌道上の任意の二点との距離の和が一定であるような定点が二つ存在し、それを「焦点」と呼ぶ
。衛星が周回する質量（地球）の重心（地心という）は、どちらかの焦点にあたる。長軸と楕円軌道の交点のうち、地心に近い側は地心との距離がもっとも近い点である。これを近地点（または近日点）と呼ぶ。地心から遠い方の交点は地心からの最遠点で
あり、これを遠地点（または遠日点）という。また、長円軌道上での軌道速度は、円軌道と違い軌道上の位置によって変化していき、近地点で最も速く遠地点で最も遅くなる*4。
長円軌道の「大きさ」を表す数値は、長軸半径である。
長軸半径が決まると、それと地心質量との関係から、軌道周期（軌道を一周するのにかかる時間）も平均軌道速度も決まる（周期の二乗と軌道長軸半径の三乗が比例する）*5。
長円軌道の形状……円と比べてどの程度「ひしゃげて」いるかを表す数値は、「離心率」である。これが１に近いほど「ひしゃげて」いる。また、真円軌道は離心率がゼロとなる。離心率は以下の式で求められる。
離心率＝軌道中心と地球（焦点）との距離÷長軸半径
以上が、長円軌道を平面的にのみ捉えた場合の基本的な術語だ。
さて、ここからようやく、噴射方向とそれによってどんな軌道に遷移するかを解説しよう。判りやすくするために、元の軌道が真円軌道であるとする。
まず、進行方向と正反対方向に噴射する（言い替えれば増速する）とどうなるか。
この場合、新しい軌道は元の円軌道の軌道高度を近地点とする長円軌道となる。新長円軌道の遠地点高度は増速が大幅であるほど高くなる。長円軌道の軌道速度は近地点で早く遠地点で遅い。そして遠地点での軌道速度は同高度での円軌道よりわずかに遅いので、遠地点でもう一度
（適切な量だけ）増速すると、そこで新しい最初の円軌道より高い高度の円軌道に移ることができる。この時の新旧の円軌道をつなぐ長円軌道がホーマン軌道と呼ばれる、もっとも効率的な遷移軌道だ。
逆に、進行方向と同じ方向に噴射する（言い替えれば減速する）とどうなるか。
この場合の新しい軌道は、元の高度を遠地点とする長円軌道となる。近地点高度は減速が大幅であるほど低くなる。このとき、近地点が大気圏上層部の比較的空気抵抗の高いところにまで低下すると急速に減速が進み地表に降りる……または墜落することになる。またさきほどと逆に、近地点で
さらに減速すればより低い円軌道に、ホーマン軌道を経由して移ったことになる。
これらを応用して、この稿の冒頭で書いた、『同じ軌道上にある二つの飛翔体、その後方の飛翔体が前方においつく』方法を解説しよう。
まず減速して、ホーマン軌道を経由して低高度軌道に移る。これで元の軌道より軌道速度が速くなるので、ここで慣性航行するうちに前方の飛翔体に「追い付く」のだ。追い付いたら、さっきと逆の経過で増速してもとの軌道に戻る。これが推進剤をもっとも効率的に使う接近法である。なお、早く追い付きたいときは、加減速をそれぞれ大きくするほど早く追い付けることになる。
以上の様に、軌道高度を変えるための噴射は、軌道上の進行方向に沿ってどちらかに噴射するしかない。軌道上の進行方向に直角な方向に噴射しても軌道高度も軌道速度も基本的に変わらない。しかし元の軌道と変化することは確かだ。
では、一体どんな軌道に移ることになるのだろうか。
まず進行方向からみて真横（進行方向にも上下方向にも垂直）に噴かすとどうなるかというと、軌道の高度も形状も変わらないが軌道面が回転することになる。言い替えれば、進行方向がそれるのである。例えば、ぴったり赤道上空にある軌道上で進行方向に真横にスラスタを噴かすと、赤道上空と２点で交差する真円軌道に移ることになる。こうやって軌道面の傾斜角を変えることができるが、これを軌道面制御という。
真下や真上に噴かすとどうなるかというと、これがちょっとややこしい。
そもそも「真上」と「真下」つまり地球の中心を通る鉛直線上に沿って噴射すると、噴射をはじめた瞬間から円軌道でなく長円軌道になるので、軌道速度に直交しないから軌道速度そのものが変化してしまう。その場合の軌道遷移の例
を左図に示すが、この新しい長円軌道は噴射したところと地心ををはさんだ対蹠点の２カ所で旧軌道と交わる。軌道制御上の効率が良くないので、「上下」成分へのスラスタ噴射は意図的な軌道遷移には使われない。ただ、「上下」方向の力を、事故や衝突等によって軌道上で受けた場合の例として掲げておく*6。
軌道上で受ける力の向きは、分解すると必ず以上３つの速度成分になるので、それを組合せればあらゆる軌道遷移を想定することができるはずである。ただし意図的なスラスタ噴射は、効率上
から進行方向そのものか、いわゆる左右（進行方向及び地心に直交する方向）に限られるため、それだけをイメージできるようになれば、『軌道傭兵』の理解には充分といえよう*7。
「軌道要素」は６つ
以上で、今回の主テーマである軌道航行のおおまかなあらましは終わる。
ただ、いままで衛星軌道の概念を、単純化した平面でのみ説明してきた。基本的な概念理解にはそれで充分なのだが、実際の衛星軌道は立体的に地球と交差しているわけで、しかも月の影響や上層大気との摩擦、太陽風や地球磁気圏などとの相互作用で、加減速をしなくてもその軌道がふらつくため、精密な運航には精密複雑な演算による軌道修正が必要であることを蛇足ながら確認しておこう。
また、衛星軌道を決定する基本的な概念・用語のうち、平面的な軌道概念については既に解説したが、軌道がつくる平面（軌道平面）がどのような角度・向きで地心（地球の重心）と交差しているかをいわなければ、本来の立体的な軌道の姿は捉えられない。
以下、衛星軌道を立体的に捉えるための要素を解説しよう。
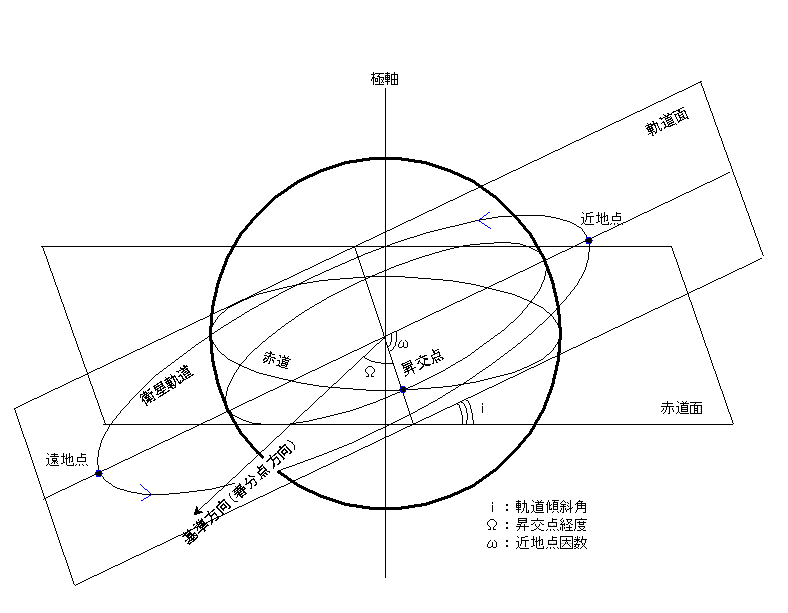
まず、基準座標について。交差する角度を測るための基準座標には、赤道面と春分点を使う。赤道面は、文字通り地球の赤道を通る平面。そして、黄道面－地球の公転面を天球上に投影した平面－と赤道面が天球上で交差する２点のうち、黄道が赤道面を南から北へよぎる点を春分点と呼ぶ。なお、春分点は牡羊座方向にある。恒星の位置を基準にした座標なのである。以下、これらと軌道面とが織りなす三種の角度で、軌道平面の立体的な位置づけをおこなう。
一つ目の角度は軌道傾斜角。これは衛星の軌道面が赤道面に対してなす角だ。
次に、昇交点経度は、昇交点（軌道が赤道面を南から北へよぎる点）を、春分点を基準とした角度（経度）であらわしたもの。
最後に、近地点因数。以上の二つが軌道面と赤道面の交差角を示したのに対し、これは軌道面の楕円長軸が、どちらを向いているかを示すもので、昇交点と近地点のなす角度を軌道面に沿って測る。真円軌道
にはこの要素は存在しない。
以上あげたもののうち、離心率、軌道長軸半径、軌道傾斜角、昇交点経度、近地点因数の５つに、近地点通過時刻を加えたものを「軌道要素」という。（軌道の六要素、ケプラーの六要素、古典軌道要素などともいう）
衛星軌道を数学的に表すためにはこれらの数値が揃っていなければならない。
なお、離心率と軌道長軸半径の代わりに近地点距離と遠地点距離－近地点・遠地点と軌道の中心との距離－を使う場合もある。離心率と長軸半径が判れば近地点と遠地点が算出できるし、その逆も同様なので、置換が可能なのである。また近地点通過時刻の代わりに平均近点離角という数値を使う場合もある。
ずいぶん複雑に見えるが、『軌道傭兵』に登場する軌道はおおむね軌道傾斜角が小さいこともあり、作品のおおまかな理解には、軌道平面と軌道遷移のイメージがとらえられれば充分といえるかもしれない。ちなみに、現有計画によるフリーダムの予定軌道は、軌道傾斜角２８．５度、高度４６０㎞の真円軌道だ。
様々な軌道
最後に、『軌道傭兵』に出てくる軌道名（分類）を一覧し、簡単に解説しよう。
参考資料：「宇宙飛行士になるための本」同文書院 宇宙開発事業団編
「人工衛星－ロケットから放送衛星まで－」電気書院 永井裕著 他
*1 ちなみに、後者の機位変更については、噴射以外の方法が想定されないでもない。ただし機体に「関節」がなければならない。機体の「関節」を曲げ伸すことによって、噴射口の向きをかなり自由に変えることが可能なのだ。ただしそれはもちろん、加減速や軌道修正には何の役にもたたない。
なお、発生した回転運動の周期を調整するには、「ヨーヨー」を使うという方法もある。一巻で秋山が使った方法だ。運動量が保存されている時、物体の回転周期は半径に反比例することを利用したわけで、
重りをぶらさげたヒモをのばすと回転周期が遅くなる。縮めると早くなる。手や身体を屈伸させるだけでもけっこう変わる。フィギュアスケートのスピンで手を屈伸することによる回転速度の変化を利用した見せ場があるのは、これの応用の一つ。
*2 本稿の最後にあるように、第二宇宙速度を越える速度を獲得できるまで加速すれば、新しい軌道は長円軌道でもなく、双曲線／放物線軌道となる。
*3 軌道速度に関連して、若干補足しておく。
地球の重力に逆らって、とりあえず衛星軌道にのるだけでも大変な速度（いわゆる第一宇宙速度。およそ秒速７．８㎞、即ち時速２８０００㎞）が必要なわけだが、この結果宇宙では大気圏飛行と比べて速度と加速能力の差が極めて大きくなる。速度成分を完全に打消すのにかかる時間が遥かに長くなるのだ。
言い替えれば、運動方向を変えることは大気圏より遥かに難しい。
既存ＳＦの宇宙戦闘シーンは、しばしばこれを（しばしば娯楽性の要請上わざと）忘れている。つまり、宇宙での飛翔体の遭遇は、よほど限定された条件が無い限り「すれ違い戦」になってしまうのだ。航行時間に対し戦闘可能時間もその想定される位置関係もごく限られており、いわゆる「格闘戦」だの海戦における「艦隊戦」の概念を適用できることはごくごく稀に違いない。そのあたりをきちんと抑えて書いて（ちゃんと小説に出来る）作家は、日本では谷甲州だけである。宇宙での飛翔体同士の相対速度をそのまま汎用兵器（航空宇宙軍史における「爆雷」）に利用するというアイデアが、どれほどリアルで必然的なものか、あらためて確認して頂きたい。
*4 いわゆるケプラーの第二法則、「面速度一定の法則」による。
*5 いわゆるケプラーの第三法則である。
*6 この時、進行方向にあくまで垂直に噴射し続けたとすると、運動エネルギーが保存され離心率が増大していくことになる。この場合は新しい軌道と旧軌道との交点の位置が、噴射点より順次ずれていくことになる。
*7 ちなみに、ステーションやシャトルから人間等が漂流してしまったり、物体をぶん投げたりしたときも、ここまでとまったく同様に考えることができる。
減速または増速になるような力を大きく受けた場合は、周期がずれてしまうので再び邂逅するのは難しくなる。（１巻で漂流した秋山が最初に気にしたのはそこだった）そうでなければ軌道周期は変わらないので、地球を１周するごとに２回、元のステーションやシャトルと接近することになる。
*8 地球の自転を最大限に利用できるので、打ち上げ基地はできるだけ低緯度である方が有利だ。『軌道傭兵』５巻で「民間打ち上げ基地が集中している」とされてる場所は、ほぼ赤道直下にある。ただ、軌道傾斜角が大きいほど、自転による初速がその軌道に生きる割合は減っていくので、極軌道衛星の場合は低緯度で打ち上げるメリットはほとんどない。
軌道傭兵研究編に戻る